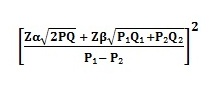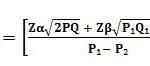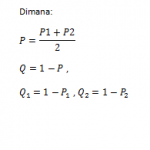Perhitungan jumlah sampel ini digunakan untuk melihat apakah ada perbedaan persentasi/proporsi sukses antar dua kelompok sampel dimana data-data awal yang diperlukan diantaranya:
i. Data historis yang menyatakan bahwa persentasi sukses pada salah satu kelompok diketahui, umumnya kelompok kontrol
ii. Tingkat signifikan uji=Z-alpha dan power pengujian = Z-betha
untuk menguji jika kedua kelompok sampel dikatakan menghasilkan proporsi sukses yang berbeda jika selisihnya proporsi antar kedua kelompok minimal sebesar P1-P2., berapa jumlah sampel minimal yang diperlukan untuk masing-masing kelompok?. Perhitungan besar sampel ini biasanya diaplikasikan pada uji klinis yang bersifat Case-Control
CONTOH UJI KLINIS
Seorang peneliti ingin mengetahui apakah terdapat perbedaan kesembuhan antara obat A (standar) dengan obat B. untuk menentukan besar sampel, peneliti menetapkan bahwa proporsi kesembuhan obat A dengan obat B dianggap bermakna jika selisihnya 20%. Diketahui bahwa kesembuhan pada obat A adalah 70%. Bila ditetapkan kesalahan tipe I sebesar 5%, kesalahan tipe II sebesar 20%, dengan hipotesis satu arah, berapakah besar sampel yang diperlukan?
Formula Yang Digunakan (Silakan Klik)
Formula Jumlah Sampel Uji Klinis Dua Proporsi Sampel
Adapun parameter yang tersedia dari contoh kasus diatas sbb:
- P2=angka kesembuahan pada obat standar = 0.7
- Q2= 1-P1 = 1- 0.7 = 0.3
- Selisih proporsi dikatakan ada perbedaan signifikan proporsi sukses dua kelompok sampel P1-P2=0.2
Dengan demikian,
- P1 = P2 + 0,2 = 0,7 + 0,2 = 0,9
- Q1 = 1 – P1 = 1 – 0,9 = 0,1
- P = (P1+P2)/2 = (0,7+0,9)/2 = 0,8
- Q = 1 – P = 1 – 0,8 = 0,2
- Kesalahan tipe I ditetapkan sebesar 5%, sehingga Za = 1,96. (dari tabel)
- Kesalahan tipe II ditetapkan sebesar 20%, makan Zβ = 0,84. (dari tabel)
Dengan memasukkan nilai nilai diatas pada rumus, diperoleh:
Jadi jumlah sampel minimal untuk masing-masing kelompok yg diberi obat A =62 orang dan kelompok yg diberi obat B= 62 orang