Metode Weighted Least Squares (WLS) adalah teknik regresi yang digunakan untuk mengatasi masalah heteroskedastisitas dalam analisis regresi. Heteroskedastisitas terjadi ketika varians error tidak konstan, yang dapat memengaruhi validitas estimasi parameter regresi. WLS bekerja dengan memberikan bobot pada data, di mana bobot tersebut biasanya proporsional terhadap invers varians error. Dengan cara ini, WLS dapat menghasilkan estimasi parameter yang lebih akurat dibandingkan metode Ordinary Least Squares (OLS) dalam kondisi heteroskedastisitas.
David A. Freedman Dalam bukunya “Statistical Models: Theory and Practice”, menekankan bahwa asumsi homoskedastisitas dan independensi residual memiliki dampak yang lebih besar terhadap validitas model regresi dibandingkan asumsi kenormalan. Menurutnya: “Normality is not required for the least-squares estimates to be unbiased and consistent. Homoskedasticity and independence of errors matter much more.” Dengan kata lain, meskipun data residual tidak normal, selama varians residual konstan (homoskedastis) dan tidak berkorelasi satu sama lain (independen), maka estimasi koefisien regresi linear tetap valid dalam konteks inferensial maupun prediktif.
Langkah-langkah analisa Regresi WLS
- Membuat analisa homokedastisitas dengan metode ….
- Membuat bobot
- Melakukan analisa regresi WLS
Contoh Aplikasi
Ingin diketahui pengaruh lama bersekolah age, income, own rent, selfemp dan imcomesq terhadap exp. Jumlah data yang dianalisa sebanyak 72 data, yang tersimpan dalam file : Data WLS.Sav
- Melakukan uji homokedastisitas dengan menggunakan metode Glejser
- Lakukan analisa Regresi
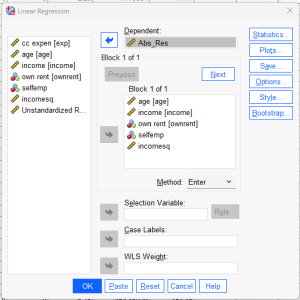
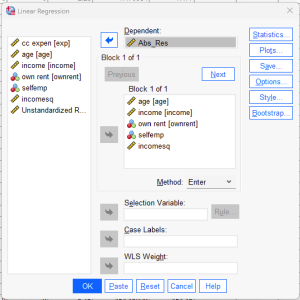
- Analyze > Regression > Linear
- Masukkan variabel dependen (exp) dan independen (age, income, own rent. Selfemp dan omcomesq.
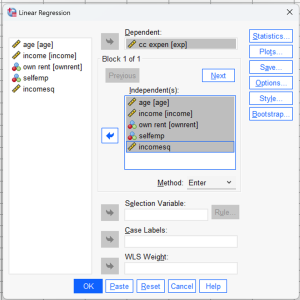
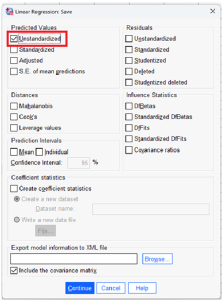
Menyimpan data residual hasil analisa regresi. Data residual merupakan selisih antara data dengan garis regresi yang terbentuk.
- Klik Save dan centang Unstandardized Residuals.
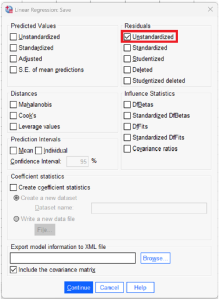
- Klik OK untuk menjalankan regresi.
Hasilnya diperoleh nilaiAdjusted R Square sebesar 0,189 atau pengaruh dependen terhadap independent sebesar 18,9%.
|
Model Summaryb |
||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .496a | .246 | .189 | 286.36819 |
| a. Predictors: (Constant), incomesq, age, selfemp, own rent, income | ||||
| b. Dependent Variable: cc expen | ||||
Variabel independent yang berpengaruh terhadap dependent variabel (cc expen) yaitu income dengan p-value 0.007, untuk variabel independent lainnya tidak nampak adanya pengaruh yang signifikan.
| Coefficientsa | ||||||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
||
|
B |
Std. Error |
Beta |
||||
| 1 | (Constant) | -242.390 | 200.763 | -1.207 | .232 | |
| age | -2.494 | 5.672 | -.056 | -.440 | .662 | |
| income | 226.993 | 82.175 | 1.213 | 2.762 | .007 | |
| own rent | 16.978 | 86.281 | .026 | .197 | .845 | |
| selfemp | -125.778 | 253.949 | -.065 | -.495 | .622 | |
| incomesq | -13.650 | 7.989 | -.757 | -1.709 | .092 | |
|
a. Dependent Variable: cc expen |
||||||
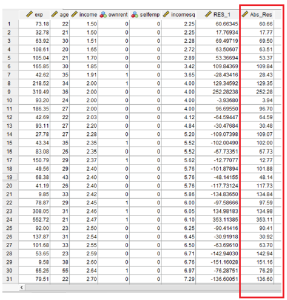
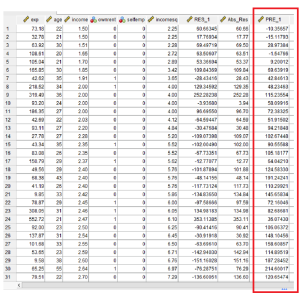
Data nilai residual hasil analisa regresi linier yang di simpan dalam file data.
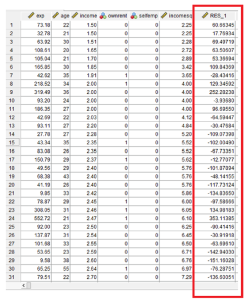
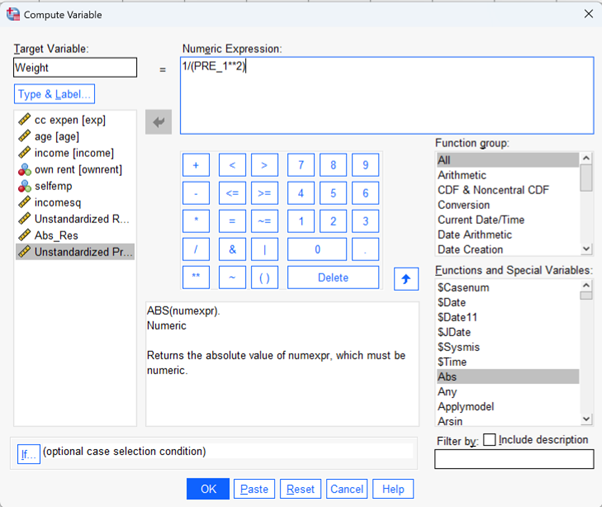
Hasil residul (RES_1) yang terbentuk kemudian dibuat ke dalam nilai mutlak (nilai negatif dirubah menjadi positif). Dengan prosedur:
Transform -> Compute Variable …
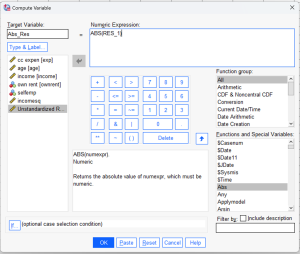
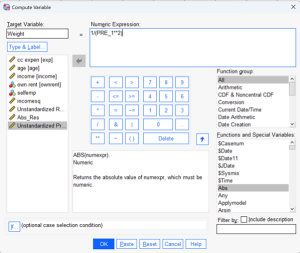
Selanjutnya pada kotak dialog “Compute Variable” yang muncul, pada kotak “Target Variable” tuliskan Abs_Res lalu pada kotak “Numeric Expression” ketikan ABS(RES_1)
Uji Homogenitas
|
Coefficientsa |
||||||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
||
|
B |
Std. Error |
Beta |
||||
| 1 | (Constant) | -329.148 | 144.983 | -2.270 | .026 | |
| age | 4.761 | 4.096 | .155 | 1.163 | .249 | |
| income | 161.316 | 59.343 | 1.245 | 2.718 | .008 | |
| own rent | -57.478 | 62.308 | -.127 | -.922 | .360 | |
| selfemp | -187.221 | 183.392 | -.141 | -1.021 | .311 | |
| incomesq | -12.414 | 5.769 | -.995 | -2.152 | .035 | |
| a. Dependent Variable: Abs_Res | ||||||
- Membuat bobot regresi
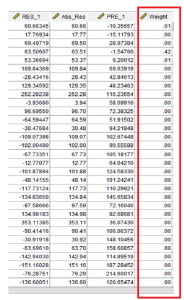
- Melakukan analisa Regresi WLS
| Model Summaryb,c | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .953a | .908 | .901 | 1.55966 |
| a. Predictors: (Constant), incomesq, own rent, age, selfemp, income | ||||
| b. Dependent Variable: cc expen | ||||
| c. Weighted Least Squares Regression – Weighted by Weight | ||||
| Coefficientsa,b | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 20.371 | 71.596 | .285 | .777 | |
| age | -9.718 | 2.371 | -.441 | -4.098 | <.001 | |
| income | 190.843 | 46.151 | 3.282 | 4.135 | <.001 | |
| own rent | 153.710 | 40.419 | .368 | 3.803 | <.001 | |
| selfemp | 47.151 | 205.126 | .096 | .230 | .819 | |
| incomesq | -11.932 | 4.936 | -2.380 | -2.417 | .018 | |
| a. Dependent Variable: cc expen | ||||||
| b. Weighted Least Squares Regression – Weighted by Weight | ||||||