Analisis multilevel, juga dikenal sebagai analisis hierarkis atau analisis linier multilevel, adalah metode statistik yang digunakan untuk memahami bagaimana variasi dalam data dapat dijelaskan dan diinterpretasikan pada beberapa tingkat hierarki atau tingkatan yang berbeda. Metode ini sering digunakan ketika data diorganisir dalam struktur hierarkis atau tingkat yang bersarang, seperti data siswa dalam kelas, karyawan dalam departemen, atau pasien dalam rumah sakit.
Tujuan utama dari analisis multilevel adalah untuk mengatasi masalah ketidakmandirian atau ketergantungan antara pengamatan yang berada dalam kelompok-kelompok yang berbeda. Dalam analisis ini, variasi yang terjadi pada tingkat yang lebih tinggi (kelompok) dan tingkat yang lebih rendah (individu) dapat dianalisis secara bersamaan, sehingga menghasilkan estimasi parameter yang lebih akurat dan interpretasi yang lebih mendalam.
Beberapa konsep penting dalam analisis multilevel meliputi:
- Level atau Tingkatan: Merupakan tingkatan hierarkis di mana data diorganisir. Contoh bisa berupa tingkat individu (misalnya, siswa), tingkat kelompok (misalnya, kelas), dan lebih tinggi lagi (misalnya, sekolah).
- Variabel Pengamatan: Variabel yang diukur pada tingkat yang lebih rendah, seperti skor tes siswa.
- Variabel Tingkat: Variabel yang diukur pada tingkat yang lebih tinggi, seperti karakteristik kelas atau sekolah.
- Variansi Antara Kelompok (Between-Group Variation): Variabilitas yang disebabkan oleh perbedaan antara kelompok.
- Variansi Dalam Kelompok (Within-Group Variation): Variabilitas yang terjadi di dalam kelompok.
- Intraclass Correlation (ICC): Mengukur seberapa besar persentase total variasi yang dijelaskan oleh variasi antar-kelompok dalam analisis multilevel.
- Model Multilevel: Model statistik yang menggabungkan variabel-variabel pada berbagai tingkatan untuk menjelaskan variasi dan hubungan di antara variabel-variabel tersebut.
Keuntungan dari analisis multilevel meliputi kemampuannya untuk memperhitungkan struktur hierarkis dalam data, mengatasi masalah autocorrelation (korelasi antar-pengamatan dalam kelompok yang sama), serta memberikan hasil yang lebih akurat dan umumnya lebih kompleks dibandingkan dengan model statistik yang lebih sederhana.
Analisis multilevel sering digunakan dalam berbagai bidang penelitian, termasuk pendidikan, psikologi, ilmu sosial, kesehatan, dan bisnis, di mana data sering kali memiliki struktur hierarkis yang perlu diperhitungkan untuk mendapatkan pemahaman yang lebih baik tentang hubungan antarvariabel.
Ilustrasi
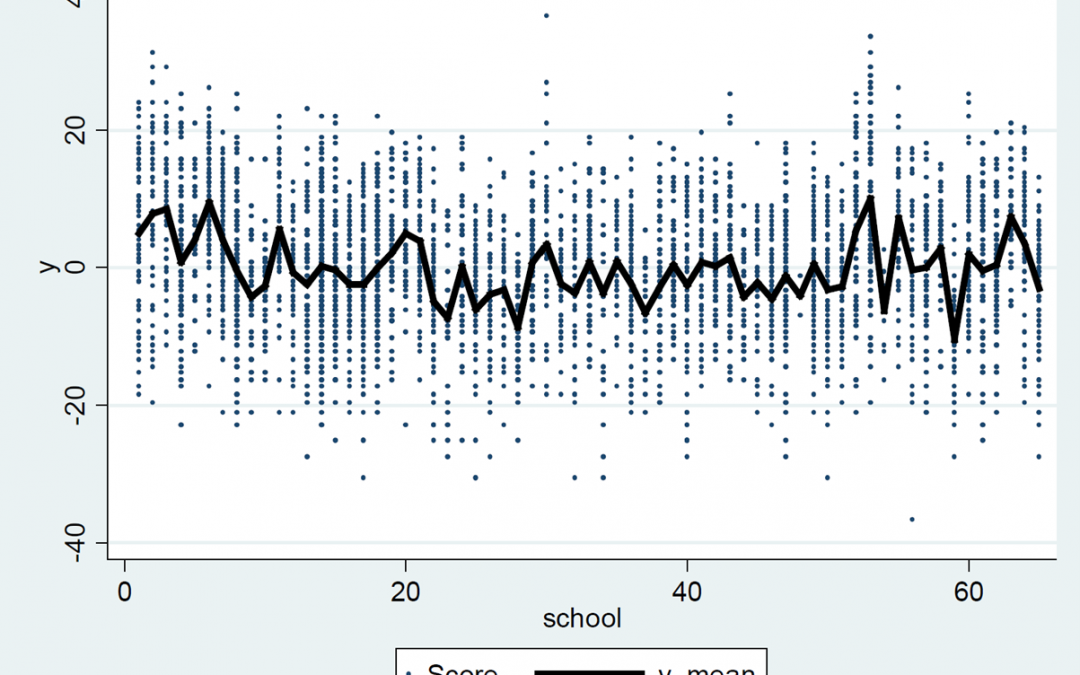
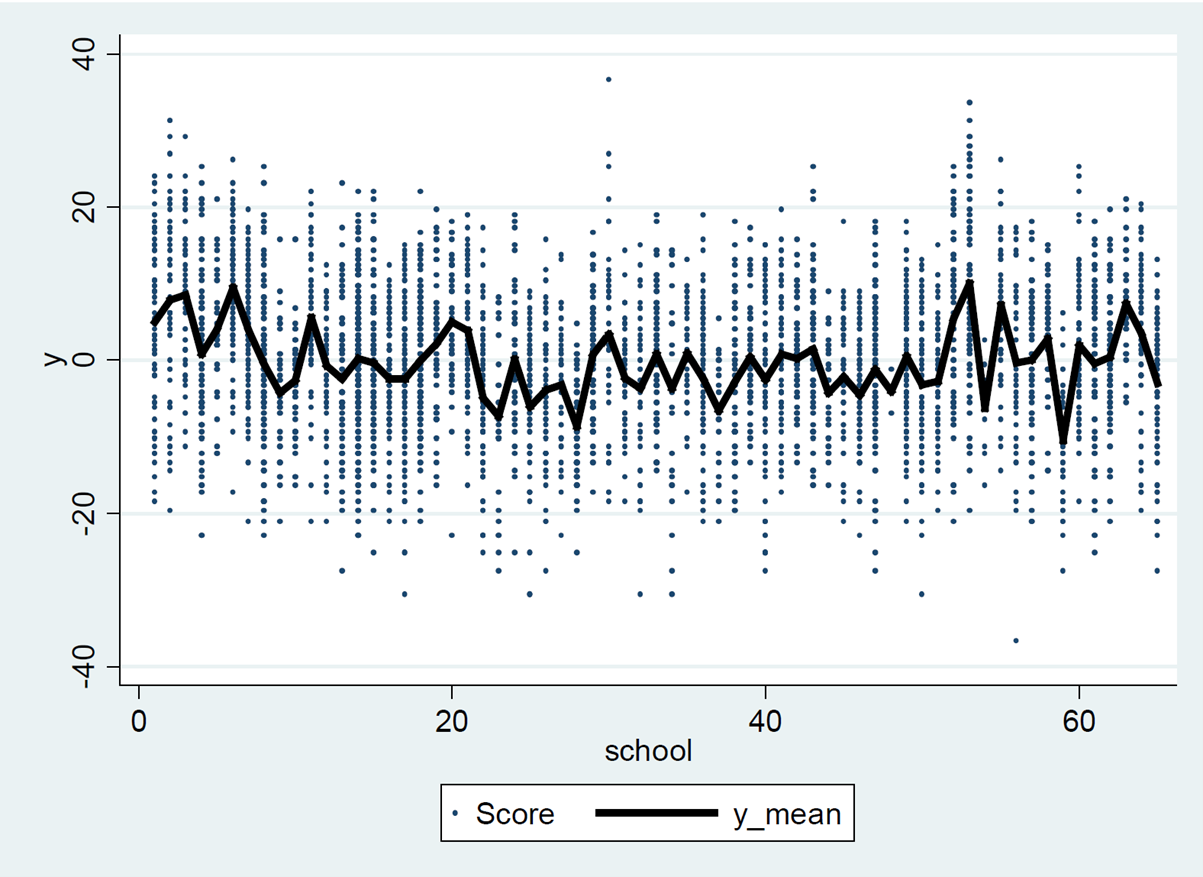
Misal ingin diketahui faktor-faktor yang berpengaruh terhadap prestasi murid sekolah dalam sebuah ujian nasional tingkat SMP. Ada sekitar 65 sekolah yang dijadikan sampel, dimana disetiap sekolah diambil sampel secara acak terkait prestasi hasil ujian mereka. Pertama-tama dihitung rata-rata prestasi secara total, kemudian dibuat grafik plot prestasi siswa di 65 sekola, dimana y=0 berarti rata-rata prestasi siswa secara total. Terlihat bahwa rata-rata prestasi disetiap sekolah ada yang baik (diatas rata-rata secara total) ada yang kurang baik (dibawah rata-rata total).
Penelitiannya ingin mengetahui faktor-faktor yang berpengaruh pada nilai prestasi belajar siswa dari:
Faktor Individu (murid) : gender, motivasi, pendidikan orang tua
Faktor Sekolah : Akreditas Sekolah, Jumlah guru tersertifikasi, jumlah penghargaan yang pernah diterima, jumlah guru honorer dll
Untuk menganalisa pengaruh faktor-faktor tersebut tentunya tidak dapat dianalisa dengan menggunakan permodelan yang umum digunakan, karena asumsi ketidak randoman dari data individu (murid) tidak terpenuhi. Analisa Multilevel menjadi salah satu metode analisa yang dapat digunakan.